Hidden Markov Models

A Hidden Markov Model (HMM) consists of a set of observed variables $X_1,…,X_n \in {1,…,m} $ and hidden variables $Z_1,…,Z_n \in {1,…,m}$. The observed variables $X_k$ can be discrete, real, anything and the hidden variables $Z_k$ are discrete. The HMM is represented by the following graphical model, called a Trellis diagram:

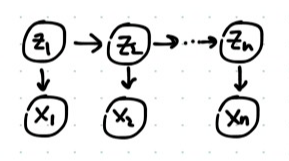
The joint distribution represented by this graphical models is:

$$p(X_1,...,X_n,Z_1,...,Z_n) = p(Z_1)p(X_1|Z_1) \prod_{k=2}^{n} p(Z_k|Z_{k-1})p(X_k|Z_k)$$

Parameters of HMM

The parameters of an HMM are the probabilities in the joint distribution above. We introduce some notation for these probabilities and give them names, but remember that they are just densities (or PMFs in discrete case).

• Transition probabilities: $T(i,j) = p(Z_{k+1}=j \vert Z_k=i) \hspace{10mm} (i,j \in {1,…,m}) $. Notice that these probabilities form a transition matrix.
• Emission probabilities: $\varepsilon_i(x) = p(X \vert Z_k=i) \hspace{10mm} (i \in {1,…,m}) $
• Initial distribution: $\pi(i) = p(Z_1=i) \hspace{10mm} i \in {1,…,m }$

With these abbreviations, we rewrite the joing density:

$$p(X_1,...,X_n,Z_1,...,Z_n) = \pi(i) \varepsilon_{Z_i}(x) \prod_{k=2}^{n} T(Z_{k-1}, Z_k) \varepsilon_{Z_k}(x_k))$$

The $\varepsilon$s are pretty much arbitrary; the structure of the graph is what gives the model power.